Light Invisible: Exploring the Electromagnetic Sprectrum

It is very humbling to contemplate the electromagnetic spectrum and the tiny sliver that encompasses the full range of colors we can perceive:

For his Chemistry Lab, Ken Costello considered this to mean that in terms of the full spectrum we are indeed... 

"The entire light spectrum (also known as the electromagnetic spectrum) spans light waves that are miles long to waves that are extremely short. The light we see (visible light) only spans about 1.5% of the entire light spectrum. So we would be legally blind considering what we could see." Experiment 7: Light as a Tool

To clarify the extent of this blindness, Ken Costello compared full spectrum perception to the color picture of a mountain scene (left) and then removed all but 1.5 percent of the color (right) to emphasize the 1.5 percent of the electromagnetic spectrum that we can actually perceive:

Clearly we are missing a lot and it is only by using powerful scientific instruments that we can find out what we are indeed missing.  The spectrum below displays the uses to which we put various wavelengths of the electromagnetic spectrum

For more on the above illustration, take the NASA Science:

Tour of the Electromagnetic Spectrum

Introduction:

 

 

Radio Waves:

 

Microwaves:

  

Infrared Waves:

 

Visible Light Waves:

 

Ultraviolet Waves:

 

X-Rays

 

Gamma Rays

But even though we humans are restricted to our narrow range of visible light, some animals are not!

ScienceAlert Article:

Birds Can See a 'Colour' Humans Can't.  Now Scientists Have Revealed This Hidden World.

The full text of the research paper by Cynthia Tedore and Dan-Eric Nilsson of the Zoological Institute, University of Hamburg:

Avian UV vision enhances leaf surface contrasts in forest environments

 

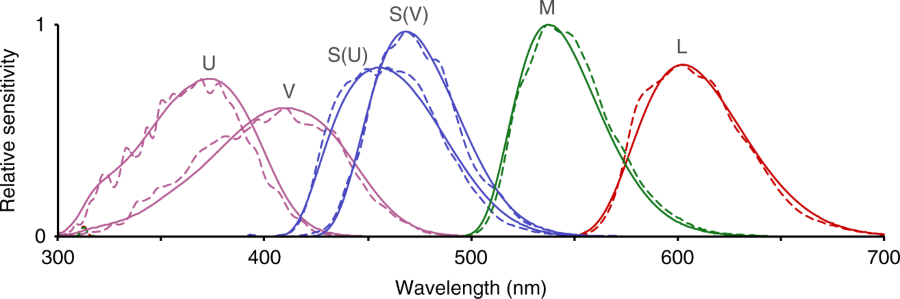
Spectral sensitivities of avian cones and multispectral camera channels. Solid lines show spectral sensitivities of avian cones and dashed lines show multispectral camera channels. Most terrestrially foraging birds are tetrachromats, having L, M, and either S(U) and U or S(V) and V cones⁶. L, M, S, V, and U stand for Long, Medium, Short, Violet, and Ultraviolet wavelengths, respectively

 

Hexaflexagons, Hexahexaflexagons, Dodecahexaflexagons and Beyond!

Preambulist [CC0], from Wikimedia Commons

Flexagons came to public attention when the late great Martin Gardner (who wrote the excellent Mathematical Games column in Scientific American) did a column on them in 1956 which included a brief history:

Martin Gardner's Flexagon Article

 
One of the clearest descriptions of the procedure for making a hexaflexagon:

wikiHow:  HOW TO MAKE A FLEXAGON 

I made a hexaflexagon of this sort from stiff card stock paper.  At first I thought that this paper might make flexing difficult, but found that it actually makes it easier to flex.  Here is a brief video in which I flex through the three sides: yellow, purple and green:

A great flexagon resource page has been provided

 by Jürgen Köller:

Jürgen Köller's Flexagon Page 

Making a Hexahexaflexagon

A hexahexaflexagon is a hexagonal flexagon with six edges which can reveal six faces.  It can be made from a single strip of paper with 19 equilateral triangles.  For mine I used the following template printed twice on 8.5x11 card stock.  I then glued the two segments together by overlapping one triangle to give the needed 19 (which includes one as a flap for gluing).  This template gives a strip that is the width of a standard roll of clear packing tape, so before folding you can cover both sides with packing tape for extra strength:

The following video presents a good numbering system for making a hexahexaflexagon:

 The next video makes clear the final crucial phase of constructing a hexahexaflexagon:  the orientation and gluing of the flaps:

St Mary's University provides a PDF template for making this particular hexahexaflexagon:

St Mary's University also has a great Web Page on Flexagons.

Here is a brief flexing tour of my hexahexaflexagon that I covered with packing tape before folding:

 

For the above hexahexaflexagon you can make the following Feynman diagram of all the possibilities paired according to the colors of the front and back of the flexagon at that point.  You will notice that each pairing of front and back is unique, so taking up your hexahexaflexagon you will immediately know where you are on the diagram and how to flex to get anywhere you wish to go. The circles in the bottom right simply show all six colors available:

In the process of making a hexahexaflexagon, Vi Hart, the queen of flexagons describes the history of flexagons including Feynman diagrams that map the flexing relations and the Tuckerman traverse that provides a topological path to all six sides of the hexahexaflexagon:

Making a Dodecahexaflexagon

The dodecahexaflexagon is a particularly fascinating elaboration of the basic hexaflexagon.  It has twelve different faces.  Michael Anttila provides an excellent walk through of the twelve faces and twenty one states of the dodecaflexagon:

 Michael Anttila also provides a step by step video on the making of his marvellous dodecahexaflexagon:

For my dodecahexaflexagon I followed the following excellent instructions from David Pleacher:

I used card stock for the base and the same template as I used for my hexahexaflexagon above.  Instead of numbers I used smaller colored paper triangles in twelve colors and covered the whole strip with clear packing tape before folding.  Here is the result:

 
 I also made a Feynman diagram for my dodecahexaflexagon.  Each circle has the colors of the front and back of the flexagon at that point.  I named the outside areas after the related colors which are the hardest ones to flex to.  All twelve colors used are show in the bottom right:

 And beyond the dodecahexaflexagon, there are many other flexagon variations to explore, such as the amazing 3D origami moving flexagon, presented by Joe on the YouTube Channel:  How to Origami... 

I followed Joe's excellent instructions and made my first 3D Hexaflexagon.  I decided to make a number of models and for this reason made a template that made accurate folding easier:

In his instructions, Joe just tucked one side into the other, but I decided to make this easier and the result less thick and more flexible by creating a glue flap instead.  I printed this template on card stock, cut it out and made my 3D Hexaflexagon with four sides:  Red, Blue, Yellow and Black:

I made another 3D Hexaflexagon using brightly colored paper glued to cardstock.  I then covered the whole sheet of paper with clear packing tape.  The packing tape made folding more difficult and it took longer to flex it in, but the result was quite good:

Icosikaitetrahexaflexagon!

The icosikaitetrahexaflexagon has 24 sides, or 24 different faces to flex to.  Here is a brief description from teacher Danny Doucette:

 

 Richard Dibbs and his friends present an excellent video of how to make the icosikaitetrahexaflexagon:

The numbering for the triangles is given in the video description:

 

Finally, cbx33 presents a fascinating and complete walk through of the icosikaitetrahexaflexagon with progress shown on an inset Feynman diagram:

 

 

Observable Universe in a Single Image

ScienceAlert Article: 

The Entire Known Universe, in a Single Image. 

Here's What It Looks Like 

Created by musician and artist Pablo Carlos Budassi, there is lots more information available in his Blog:

Observable Universe Logarithmic Illustration Blog

  The entire observable Universe can be featured because the distance scale diminishes exponentially the further you go out from the Earth according to the following scale:

This scale is featured on the version of the illustration that features helpful labels:

Further information on the logarithmic projection for maps is provided by Philippe Rivière including an interactive sample projection centered on Iceland which can be observed as variables are altered:

 The Log-Azimuthal projection

As we look further and further away we also look further and further back in time since light although fast, does take time to travel long distances.   NASA scientist James O'Donoghue created some animations to help visualize the speed of light:

First, light is able to travel 7.5 laps around the Earth every second:

Next we see how long it takes light to go from the Earth to the Moon:

Finally we see how slowly light travels the greater distance from Earth to Mars:

The Amazing Antikythera Mechanism

Astoundingly intricate astronomical mechanism retrieved by divers from 45 metres (148 ft) of water in the Antikythera shipwreck off Point Glyphadia on the Greek island of Antikythera (pronounced an-ti-KEE-thur-a) in 1901, and subsequently dated to sometime in the first two centuries BC.  
 
Archeology recovers a certain picture of the past, but can be lopsided if taken to give the full picture! Too much of the past has simply not survived the rigors of time as we realize when things like this miraculously do survive.  Ancient writings mention devices like this, but none of them or their plans have survived.

Exploded computer reconstruction of the Antikythera Mechanism

 "On the left, the front plate includes zodiac and calendar dials and a conjectural reconstruction of the ancient Greek Cosmos. In the middle is an exploded reconstruction of the gears. The input contrate gear is in the centre, with a keyway to turn the Mechanism. The planetary gearing at the front is conjectural, but the gearing behind the main plate for the lunar anomaly mechanism and the back dials is now firmly established. On the upper right is the 19-year Metonic calendar dial and on the lower right, the 223-month Saros eclipse prediction dial."

A schematic representation of the gearing of the Antikythera Mechanism, including the latest published interpretation of existing gearing, gearing added to complete known functions and proposed gearing to accomplish additional functions, namely true sun pointer and pointers for the five then-known planets, as proposed by Freeth and Jones, 2012.

Describing the genesis of this computer reconstruction, here is the research paper written by Tony Freeth and Alexander Jones:

The Cosmos in the Antikythera Mechanism

This video is a tribute from Swiss clock-maker Hublot and film-maker Philippe Nicolet to this device, known as the Antikythera Mechanism, or the world's "first computer":

Wikipedia article on the Antikythera mechanism

Virtual model of the Antikythera Mechanism by Mogi Vicentini based on the theoretical and mechanical model by Michael Wright:

Washington Post Article: The world’s oldest computer is still revealing its secrets

Smithsonian Article:  Decoding the Antikythera Mechanism, the First Computer

Quote from the end of the above article:  

Antikythera mechanism proves that the ancient Greeks used complex arrangements of precisely cut wheels to represent the latest in scientific understanding. It’s also a window into how the Greeks saw their universe. They came to believe that nature worked according to predefined rules, like a machine—an approach that forms the basis of our modern scientific views. Edmunds argues that this “mechanical philosophy” must have developed as a two-way process. The ancient mechanics who captured the cosmos in bronze weren’t just modeling astronomical theories but were also inspiring them.

NOVA Documentary:  Antikythera Mechanism The Two Thousand Year Old Ancient Computer:

 

Research from 2021 on the front of the mechanism:

A Model of the Cosmos in the ancient Greek Antikythera Mechanism

 

Fascinating Science of the Trebuchet

The Trebuchet is an intriguing medieval device for flinging rocks and other projectiles.  It differs from a catapult insofar as it does not use torsion or bending, neither the bending of wood (such as a bow or ballista) nor the torsion of twisted ropes (often seen in Roman catapults).  It can be built on huge scales to heave heavy boulders and other massive projectiles.

The Trebuchet Store has a good basic summary of 

How a Trebuchet Works

They also provide an good animated drawing of a hinged counter-weight trebuchet in action:

Perhaps the best way to get to know the trebuchet (considered the most powerful medieval siege engine) is to build one yourself.  There are many kits available.  A free one that you can make using print-outs on card stock is available from 

Fryer's Kits

One to purchase inexpensively (compared to some kits!) which I have built and can recommend is 

 Pathfinder Hinged Counter-Weight Trebuchet

 

The Pathfinder Trebuchet under construction.  At this point I had glued and pegged together the frame and base as well as the counter-weight box which will eventually be filled with stones.  The pegging is done for added strength.  At this point the building instructions say to stop and have a snack!

And now the completed model on the dining room floor with special guest star William Shakespeare to suggest the approximate human scale:

And in another close-up picture:

From the dining room floor I was able to hurl a grape into the kitchen, a distance of about 20 feet or 6 meters.

Here is a fun video of a family using the Pathfinder trebuchet on their back deck (and includes a helpful warning about the dangers of standing directly behind the trebuchet):  

Once constructed you can make some adjustments to try and get the maximum firing range.  You can add or remove stones from the counter-weight box.  You can change the length of the string that runs from the sling pouch (that holds the grape) to the top of the throwing arm.  

A Virtual Trebuchet is handy to see how changing these various parameters can affect the throwing.  Just set the parameters and press the SUBMIT button to fire the trebuchet:

Online Virtual Trebuchet 

My own fascination with trebuchets was inspired by the excellent article that appeared in Scientific American:

The Trebuchet

It is also helpful to watching the firing of a full scale trebuchet such as the one we watched being fired in Provence, France:

Or check out what is considered to be the world's biggest trebuchet in action at Warwick Castle:

Daily Planet documents the largest trebuchet in continental Europe and the difficult process of adjusting the firing range:

One of the reasons I started watching the great series Northern Exposure (about a young New York doctor exiled to a small Alaskan community) was that I read they had actually built a trebuchet capable of hurling an old upright piano... 

      

 

There are many interesting trebuchet videos on YouTube, including the following fascinating experimentation with both fixed and hinged counter-weights:

Trebuchets have appeared in TV shows and movies.  The Historian on the Warpath has critiqued a few.  First the Game of Thrones trebuchet that appears during the Battle of the Bastards:

Problems with the Game of Thrones Trebuchet 

The Game of Thrones trebuchet was apparently based upon an amazing trebuchet named Merlin that was actually built and fired:

 Historian on the Warpath also critiqued the Boulder Machine Gun Trebuchet that was used in the Chronicles of Narnia:

Trebuchets on Screen: Chronicles of Narnia