 |
| From: Movies of the Periodic Planar Collisionless Three-Body Orbits |
Predicting eclipses was important to many ancient peoples and involved trying to understand the combined motions of three celestial bodies: the sun, the earth and the moon. This was the beginning of the the famous Three Body Problem that received its modern scientific formulation in Newton's Principia (Book 1 - Proposition 66):
Let three bodies—whose forces decrease as the squares of the distances—attract one another, and let the accelerative attractions of any two toward the third be to each other inversely as the squares of the distances...
Newton wrote to Edmond Halley that the theory of the motions of the moon made his head ache and kept him awake so often that he would think of it no more, but this problem was now out there to tantalize mathematicians and astronomical physicists. Others soon wanted to solve the more general three body problem and also came up against intractable difficulties and complications that finally led the great mathematician Henri Poincare to conclude that even varying the initial conditions of the three bodies in the very smallest ways would lead to vastly different results. This led to the development of Chaos Theory, the popular example of which is the idea of flapping butterfly's wings in one place leading to a tornado in another place.
Solving the Three Body Problem - hosted and written by Matt O'Dowd (PBS Space Time Series)
Though many great mathematicians could not solve the three body problem, they did make progress by finding more and more examples of stable, periodic orbit configurations.
Leonard Euler the great 18th century mathematician began this trend by finding periodic solutions where the three bodies are collinear, or in a row or straight line:
Lagrange continued this trend by finding stable configurations when the three bodies are configured at the vertices of an equilateral triangle.
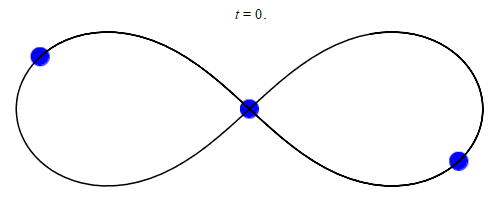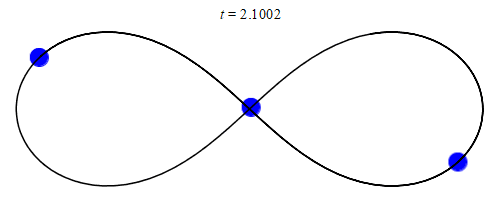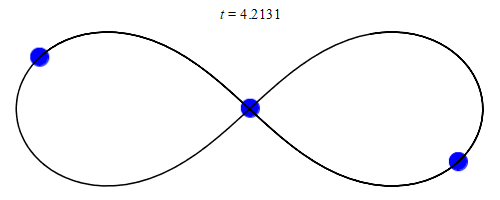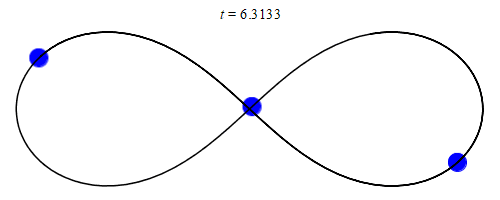
In 1993, a solution with three equal masses moving around a figure-eight shape was discovered by physicist Cris Moore at the Santa Fe Institute:
Today, physicists and mathematicians continue to search for and find further special case solutions:
The Institute of Physics Belgrade has a great website for exploring these solutions:
Institute of Physics Belgrade
A good example from this gallery shows how the figure-eight configuration of Cris Moore is mapped onto the shape sphere:
The shape sphere provides a kind of condensed version of the orbits.
For example, try to image if we had to represent numbers just as a bunch of dots. Works well for low numbers, but is totally unwieldy and confusing for large numbers. So the decimal system was developed as a condensed representation for numbers, and it is a system that itself reveals a lot more about a number than a bunch of dots ever could!
Likewise shape sphere representations of stable three body configurations give us some help in dividing these configurations into families.
The three red dots on the equator of a shape sphere represent the three possible collision points: body 1 with 2, body 2 with 3 and body 3 with 1. Needless to say all stable three body configurations will studiously avoid these three points!
As a side light: the shape sphere was first mentioned in James Joyce's novel Finnegans Wake (p. 295) where we see: "As Great Shapesphere Puns it." You can view this page of the Wake at the Internet Archives:
In 2017 XiaoMing Li and ShiJun Liao (at Shanghai Jiaotong University, China) used a supercomputer to hit the three body jackpot:
Many of these periodic three body orbits are stunningly beautiful and mesmerizing to see in action, and you can now watch animated gifs of them in all their glory:
Here are a few examples from the above set:
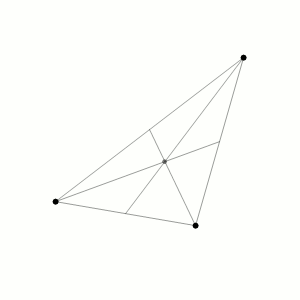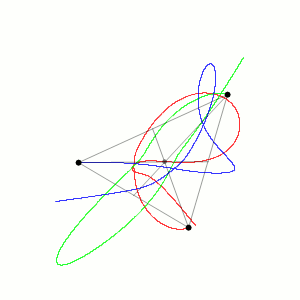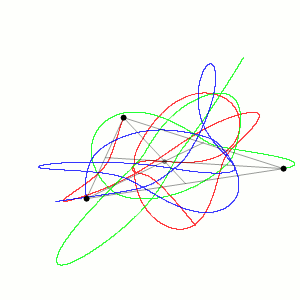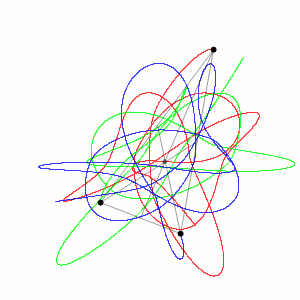
The orbit lines for the example below (and many others) seem to present a 3-D diagram, but this is an illusion! The orbit paths are all in fact on a flat plane.
No comments:
Post a Comment